On-Line Scientific Calculator

You need JavaScript switched on your browser for this to work. This mostly appears to work, and has a few quirks you have to get used to. After each calculation, click on the "Clear display" button.

Mini-Manual for this calculator

Key	Meaning	Example
deg/rad/gra	switch to degrees/radians/gradians
√x	find the square root of x	√9 = 3
x²	find x squared	6² = 36
x³	find x cubed	2³ = 8
eª	find the natural number, e, raised to the power a	e⁰ = 1 e¹ = 2.1718 e² = 7.389
log	find the base-10 log of a number	log 1 = 0 log 2 = 0.3010 log 10 = 1 log 100 = 2 100 = 10²
ln	find the natural log of a number	ln 1 = 0 ln 2 = 0.6931 or 2 = e^0.6931
lg	find the base-2 log of a number	lg 1 = 0 lg 2 = 1 lg 3 = 1.0986 lg 4 = 2 4 = 2²
sin/cos/tan	Find the sine, cosine or tangent of an angle
asin/acos/atan	Find the arcsine, arccosine, or arctangent of an angle. This is the reverse process of sin/cos/tan.
ran	Generate a random number between 0 and 1 (pseudo random).
rnd	Round the displayed number to the nearest integer.
pow	Raise some number x to the power y. Pressing "pow" clears the display for your next number.	4 pow 3 = 64 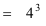$4cubed$ 2 pow 5 = 32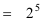 $2othe5$ 3 pow 2 = 9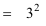 $3squared$
e	Display the number e (natural number)	e = 2.71828
π	Display the number π (Pi)	π = 3.14159
STO/RCL	Store a number in memory / Recall a number from memory
M+	Add displayed number to memory
M-	Subtract displayed number from memory

Bugs, features, bug features, and buggy features :-)

Entering simple math expressions such as 3*(9+1)/2 entirely from the keyboard (parentheses included) directly into the text box works as far as I have been able to test.
Entering a mixture of keyboard expressions and web form expressions will not always get desired results.
Entering javascript expressions such as log(25) results in nothing being evaluated. Strangely enough, no error either.
(Quote from the FVWM manpage (Linux)) Initially there were exactly 71.8 unidentified bugs. Since then 22.825 bugs have been fixed. Assuming that there are at least 10 unidentified bugs for every identified one, that leaves us with 71.8 - 22.825 + 10 * 22.825 = 277.225 unidentified bugs. If we follow this to its logical conclusion we will have an infinite number of unidentified bugs before the number of bugs can start to diminish, at which point the program will be bug-free. Since this is a computer program infinity = 3.4028e+38 if you don't insist on double-precision. At the current rate of bug discovery we should expect to achieve this point in 4.27e+27 years. I guess we better plan on passing this thing on to our children...

deg	rad	gra